Finding the antiderivatives of figures often look difficult and can confuse the students as well. The systems like Mathematica and Maxima provide us with the central theme of antiderivatives symbolically.
But the main idea behind solving this problem is never told by this computer algebra system (CAS). It is not understandable by humans, as a very complex calculation is used and gives no closure in the end.
Before going into the details, let’s talk about antiderivatives and their function in mathematics.
What are antiderivatives?
Before understanding the antiderivatives, it is necessary to know derivatives and their calculus work.
A derivative is the rate of change of function that varies concerning its variable. It is the slope of a tangent line that exists in the graph. The term antiderivative is the reverse of it. It is a function that helps to reverse the derivation of a value.
One function may have many antiderivatives that are a vital part of indefinite integrals. Finding the antiderivatives directly is not so simple as finding the large and complex values may be complicated.
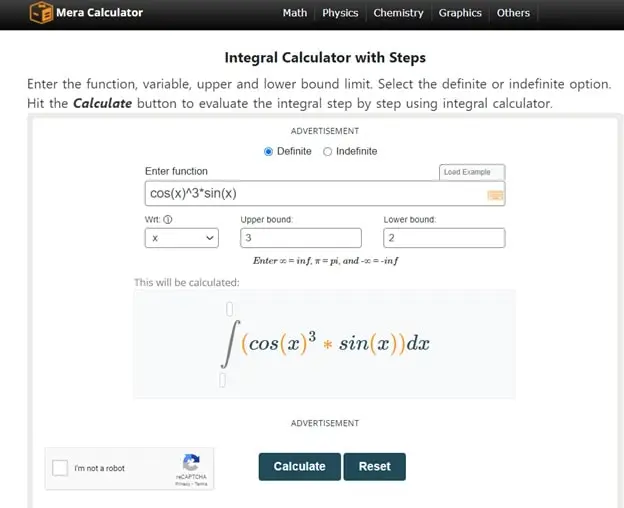
These can be found quite easily by using an antiderivative calculator that provides steps to make it more understandable.
How does the integration rule help to find antiderivatives?
An integral is a mathematical equation that helps find the area, displacement, volume, or other tiny parts. The whole process is called integration, and by following this process, we can also find the antiderivative of any number.
To find the antiderivatives using the integration rule, one can follow four different methods. By every process, he can get the same answer with additional steps.
- Power rule
- Sum rule
- Constant coefficient rule
- Difference rule
It can be challenging to understand these rules directly, so one can use any calculator that provides the step to make it more understandable.
Applying the formula with the integral calculator can get the results in steps.
1. Power rule
A power rule in integration is the inverse of the power rule that we use in the differentiation.
Let’s we have to find the integral indefinite of x2 by using the power rule. We can do it by adding values to the equation
| ∫ | ax n dx = a | x n+1 | + C |
| n+1 |
2. Sum rule
This rule helps find the derivatives of an equation by adding the number of digits that are the sum of several times.
It integrates each term separately and gets a result by following a formula.
ʃ [f(x) + g(x)] dx = ʃ [f(x)] dx + ʃ [g(x)] dx
It is essential to know that the sum of two digits is measured to be its own correct function.
3. Constant coefficient rule
The constant-coefficient rules explain the indefinite integral of “c . f(x)”, where c is the constant and f(x) is the function value.
ʃ [k *f(x)] dx = k ʃ [f(x)] dx
It ignores the constant coefficient in the value, integrates the rest of the value, and finds its antiderivatives.
4. Difference rule
This rule talks about the values that differ in two or more terms. Same as the “sum rule,” it also integrates the values separately to find their antiderivatives.
ʃ [f(x) – g(x)] dx = ʃ [f(x)] dx – ʃ [g(x)] dx
How to solve antiderivative problems using integration rules?
To learn how to calculate problems of antiderivatives, follow the below examples.
Example 1
Integrate the given function with respect to “x”.
f(x) = 3x3 + 4x7 – 2x5 + 2x
Solution
Step I: Take the given function and apply the integration notation to it.
ʃ f(x) dx = ʃ [3x3 + 4x7 – 2x5 + 2x] dx
Step II: To integrate the above expression, first of all, separate each function and apply the integration notation to it with the help of difference & sum laws.
ʃ [3x3 + 4x7 – 2x5 + 2x] dx = ʃ [3x3] dx + ʃ [4x7] dx – ʃ [2x5] dx + ʃ [2x] dx
Step III: Now take out the constant coefficients outside the integral notation.
= 3ʃ [x3] dx + 4ʃ [x7] dx – 2ʃ [x5] dx + 2ʃ [x] dx
Step IV: Integrate the above expression with the help of power and trigonometry laws of integration.
= 3 [x3+1 / 3 + 1] + 4 [x7+1 / 7 + 1] – 2 [x5+1 / 5 + 1] + 2 [x1+1 / 1 + 1] + C
= 3 [x4 / 4] + 4 [x8 / 8] – 2 [x6 / 6] + 2 [x2 / 2] + C
= 3/4 [x4] + 4/8 [x8] – 2/6 [x6] + 2/2 [x2] + C
= 3/4 [x4] + 1/2 [x8] – 1/3 [x6] + 1 [x2] + C
= 3x4/4 + x8/2 – x6/3 + x2 + C
Example 2
Calculate the new function by integrating the given function with respect to “r”.
f(r) = 2r4 + 3r2 – 12r5 + 15sin(r) + 2r
Solution
Step I: Take the given function and apply the integration notation to it.
ʃ f(r) dr = ʃ [2r4 + 3r2 – 12r5 + 15sin(r) + 2r] dr
Step II: To integrate the above expression, first of all, separate each function and apply the integration notation to it with the help of difference & sum laws.
ʃ [2r4 + 3r2 – 12r5 + 15sin(r) + 2r] dr = ʃ [2r4] dr + ʃ [3r2] dr – ʃ [12r5] dr + ʃ [15sin(r)] dr + ʃ [2r] dr
Step III: Now take out the constant coefficients outside the integral notation.
= 2ʃ [r4] dr + 3ʃ [r2] dr – 12ʃ [r5] dr + 15ʃ [sin(r)] dr + 2ʃ [r] dr
Step IV: Integrate the above expression with the help of power and trigonometry laws of integration.
= 2 [r4+1 / 4 + 1] + 3 [r2+1 / 2 + 1] – 12 [r5+1 / 5 + 1] + 15 [-cos(r)] + 2 [r1+1 /1 + 1] + C
= 2 [r5 / 5] + 3 [r3 / 3] – 12 [r6 / 6] + 15 [-cos(r)] + 2 [r2 / 2] + C
= 2/5 [r5] + 3/3 [r3] – 12/6 [r6] – 15 [cos(r)] + 2/2 [r2] + C
= 2/5 [r5] + 1 [r3] – 2 [r6] – 15 [cos(r)] + 1 [r2] + C
= 0.4r5 + r3 – 2r6 – 15cos(r) + r2 + C
Final words
To find antiderivatives, you have to follow simple steps that reverse the derivative rules. But to take help from the integration rule, you have to follow different steps. The regulations mentioned above help to get antiderivatives by various methods.

Rahul Kumar is a passionate educator, writer, and subject matter expert in the field of education and professional development. As an author on CoursesXpert, Rahul Kumar’s articles cover a wide range of topics, from various courses, educational and career guidance.